Value at Risk: Ένα νέο μεθοδολογικό πλαίσιο για την εκτίμηση χρηματοοικονομικών κινδύνων

Η πολυπλοκότητα του σύγχρονου χρηματοοικονομικού περιβάλλοντος και το πλήθος των διαθέσιμων επενδυτικών επιλογών (μετοχές, ομόλογα, παράγωγα, κά.) καθιστούν πλέον ιδιαίτερα δύσκολη τη μέτρηση του επενδυτικού κινδύνου. Παράλληλα, στα πλαίσια ανάπτυξης ρυθμιστικών κανόνων για τη λειτουργία των χρηματοπιστωτικών ιδρυμάτων και τους κινδύνους που αναλαμβάνουν έχει αναπτυχθεί ένας γενικός προβληματισμός σχετικά με την κατάλληλη μεθοδολογία ποσοτικοποίησης των κινδύνων αυτών.

Για πολλά χρόνια, στη χρηματοοικονομική διοίκηση επιχειρήσεων (Corporate Finance) και στη θεωρία των χρηματοοικονομικών αγορών (Financial Markets Theory) η έννοια του κινδύνου ήταν συνυφασμένη με τρεις βασικές στατιστικές έννοιες: (α) την αναμενόμενη απόδοση (μέση τιμή), (β) την πιθανή απόκλιση από την αναμενόμενη απόδοση (τυπική απόκλιση) και (γ) το συντελεστή μεταβλητότητας (τυπική απόκλιση/ μέσος). Ο προσδιορισμός αυτών των τριών στατιστικών μεγεθών από ιστορικά δεδομένα εθεωρείτο ότι παρείχε επαρκή πληροφόρηση σχετικά με το επίπεδο του αναλαμβανόμενου κινδύνου. Η ανάπτυξη όμως νέων πολύπλοκων χρηματοοικονομικών προϊόντων όπως τα παράγωγα, καθιστά δύσκολη την εφαρμογή αυτής της «κλασικής» προσέγγισης.

Στη δεκαετία του 1990 υπήρξε μια σημαντική εντατικοποίηση της έρευνας για την ανάπτυξη νέων μεθοδολογικών εργαλείων μέτρησης των χρηματοοικονομικών κινδύνων. Ένα από τα βασικά αποτελέσματα της έρευνας αυτής ήταν η ανάπτυξη της προσέγγισης Value at Risk (VaR) η οποία αποτελεί σήμερα ένα από τα σημαντικότερα ποσοτικά εργαλεία που χρησιμοποιούνται διεθνώς από χρηματοπιστωτικούς οργανισμούς για την εκτίμηση των χρηματοοικονομικών τους κινδύνων, ενώ παράλληλα αποτελεί σημαντικό πεδίο μελέτης από τους χρηματοοικονομικούς ερευνητές. Η διάδοση της VaR ξεκίνησε με την ανάπτυξη του συστήματος RiskMetrics από την Αμερικανική επενδυτική τράπεζα J.P. Morgan. Η ανάπτυξη του συγκεκριμένου συστήματος από την τράπεζα αυτή αποσκοπούσε στην ανάπτυξη και εφαρμογή ενός εργαλείου για τη μέτρηση και παρακολούθηση των καθημερινών αναμενόμενων ζημιών της τράπεζας από όλες τις επενδυτικές θέσεις που είχε αναλάβει. Η απόφαση της τράπεζας να εκμεταλλευτεί εμπορικά το σύστημα RiskMetrics σε συνδυασμό με τη δημοσιοποίηση της προσέγγισης στην οποία βασίζεται, έδωσαν ώθηση στην έρευνα και πρακτική εφαρμογή υποδειγμάτων VaR.

Σήμερα σημαντικοί ρυθμιστικοί κανόνες για τη λειτουργία των χρηματοπιστωτικών ιδρυμάτων που έχουν αναπτυχθεί από την Επιτροπή της Βασιλείας, την Τράπεζα Διεθνών Διακανονισμών και την Ευρωπαϊκή Ένωση προβλέπουν τη χρήση υποδειγμάτων VaR από τα χρηματοπιστωτικά ιδρύματα για την εκτίμηση των χρηματοοικονομικών τους κινδύνων.

Εκτίμηση κινδύνου

Η έννοια της VaR απαντά με άμεσο τρόπο στο πρόβλημα της εκτίμησης του κινδύνου βοηθώντας τον αναλυτή να προσδιορίσει τη μέγιστη αναμενόμενη ζημία που μπορεί να υποστεί σε ένα δεδομένο χρονικό διάστημα με κάποιο βαθμό εμπιστοσύνης, το οποίο συνήθως ορίζεται στα επίπεδα του 95% ή 99%. Για παράδειγμα, εάν η VaR μιας επένδυσης σε μετοχές είναι -10.000€ για χρονικό διάστημα μιας ημέρας με επίπεδο εμπιστοσύνης 95%, αυτό πρακτικά σημαίνει ότι υπάρχει μόνο 5% πιθανότητα η ημερήσια ζημία από την επένδυση να υπερβεί το ποσό των 10.000€. Προφανώς αυτή η πληροφορία προσδιορίζει με άμεσο και κατανοητό τρόπο τον κίνδυνο που αναλαμβάνει ο επενδυτής.

Γραφικά η έννοια της VaR αποδίδεται στο Σχήμα 1, στο οποίο παρουσιάζεται μια υποθετική κατανομή των ζημιών/κερδών μιας επένδυσης ανάλογα με την πιθανότητα εμφάνισής τους. Η VaR προσδιορίζεται ως το σημείο του οριζόντιου άξονα (κέρδος/ζημία) για το οποίο η γραμμοσκιασμένη περιοχή στο αριστερό άκρο της καμπύλης έχει εμβαδόν μικρότερο από 1-α, όπου α είναι το επιθυμητό επίπεδο εμπιστοσύνης. Εάν θεωρηθεί ότι τα αποτελέσματα της επένδυσης (κέρδη/ζημίες) κατανέμονται συμμετρικά γύρω από μια μέση τιμή κατά τον τρόπο που παρουσιάζεται στο Σχήμα 1 (κανονική κατανομή), τότε η VaR σε επίπεδο εμπιστοσύνης 95% υπολογίζεται σύμφωνα με τον τύπο -1,65σP (P είναι το ύψος της επένδυσης και σ είναι η τυπική απόκλιση των αποτελεσμάτων της επένδυσης από τη μέση τους τιμή), ενώ σε επίπεδο εμπιστοσύνης 99% χρησιμοποιείται ο τύπος -2,33σP.

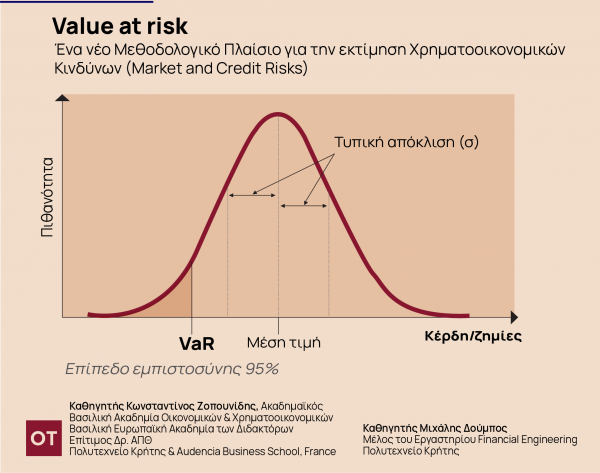
Βέβαια, στην πράξη ο υπολογισμός της VaR δεν είναι πάντα μια απλή διαδικασία, ιδίως στην περίπτωση πολύπλοκων επενδυτικών θέσεων σε παράγωγα (δικαιώματα προαίρεσης και συμβόλαια μελλοντικής εκπλήρωσης) για τα οποία δεν υπάρχουν επαρκή ιστορικά δεδομένα. Στις περιπτώσεις αυτές η υψηλή υπολογιστική ισχύς των σύγχρονων συστημάτων υπολογιστών αποτελεί σημαντικό εργαλείο για τον ακριβή υπολογισμό της VaR. Η διαδικασία που ακολουθείται αφορά την προσομοίωση στον υπολογιστή της συμπεριφοράς κάθε επενδυτικής θέσης βάσει ενός μεγάλου αριθμού κατάλληλα ανεπτυγμένων σεναρίων σε σχέση με τις μεταβολές που παρατηρούνται στην αξία του υποκείμενου προϊόντος (μετοχές, δείκτες, συναλλαγματικές ισοτιμίες, επιτόκια ομολόγων, κλπ.).

Η μεθοδολογική προσέγγιση της VaR δεν περιορίζεται όμως μόνο στην εκτίμηση του κινδύνου της αγοράς (market risk) ο οποίος προκύπτει από συγκεκριμένες επενδυτικές θέσεις. Ταυτόχρονα έχει εφαρμογή και στην εκτίμηση του πιστωτικού κινδύνου (credit risk) ο οποίος προκύπτει από τις χρηματοδοτήσεις επιχειρήσεων και καταναλωτών που παρέχει ένας χρηματοπιστωτικός οργανισμός. Στην περίπτωση αυτή υποδείγματα VaR χρησιμοποιούνται για την εκτίμηση της μέγιστης αναμενόμενης ζημίας που προκύπτει από το χαρτοφυλάκιο χορηγήσεων ενός χρηματοπιστωτικού οργανισμού σε δεδομένο χρονικό διάστημα με κάποιο βαθμό εμπιστοσύνης. Η ζημία αυτή προφανώς προέρχεται από πελάτες οι οποίοι δεν είναι σε θέση να εξυπηρετήσουν με συνέπεια τα δάνειά τους. Η χρησιμοποίηση υποδειγμάτων VaR σε συνδυασμό με αποτελεσματικές μεθοδολογίες για την εκτίμηση της δανειοληπτικής ικανότητας των πελατών παρέχουν ένα ισχυρό εργαλείο διαχείρισης χαρτοφυλακίων χορηγήσεων (βλ. Κ. Dowd, Beyond Value at Risk: The New Science of Risk Management, John Wiley and Sons, Chichester, 1998).

Συμπερασματικά, η δυνατότητα που προσφέρουν τα υποδείγματα VaR για την εκτίμηση τόσο του κινδύνου της αγοράς όσο και του πιστωτικού κινδύνου αποτελεί ένα σημαντικό πλεονέκτημα της νέας αυτής μεθοδολογικής προσέγγισης, επιτρέποντας τη συνολική ανάλυση των χρηματοοικονομικών κινδύνων που αναλαμβάνουν οι χρηματοπιστωτικοί οργανισμοί (βλ. C. Zopounidis, E. Galariotis, Quantitative Financial Risk Management, Wiley, Ed., 2015).

* Καθηγητής Κωνσταντίνος Ζοπουνίδης, Ακαδημαϊκός, Βασιλική Ακαδημία Οικονομικών & Χρηματοοικονομικών,Βασιλική Ευρωπαϊκή Ακαδημία των Διδακτόρων, Επίτιμος Δρ. ΑΠΘ, Πολυτεχνείο Κρήτης & Audencia Business School, France

* Καθηγητής Μιχάλης Δούμπος, Μέλος του Εργαστηρίου Financial Engineering Πολυτεχνείο Κρήτης